Razlomci – kako ih što lakše savladati?

Kako ih što lakše savladati?

Dok pišem ovaj tekst palo mi je napamet nešto baš zanimljivo : bi li ti bilo lakše da umjesto izraza „razlomci“ koristim izraz „RAZLOMLJENI BROJEVI“? Sigurna sam da bi. E, baš to sam primijetila u radu s djecom  - velika većina njih čak i svlada gradivo, a da uopće nisu zapravo shvatili ni vizualizirali što razlomci prikazuju. Odlučila sam upravo to malo više pojasniti u tekstu koji slijedi. 

Rijetko ćete sresti dijete koje će reći :“ Ma, razlomci su prelagani!“. Razlomci su veliko i kompleksno gradivo u matematici. Veliki je broj djece koja muku muče s razlomcima od 5. do 8. razreda ( a i kasnije, u srednjoj školi ). Ima naravno i onih koji brzo i lako shvate razlomke – svaka vam čast, djeco! Zašto je to tako i treba li možda promijeniti način na koji se djecu poučavaju razlomci?

Što su razlomci?

U 5. razredu osnovne škole uvodi se gradivo RAZLOMCI. Nakon što djeca usvoje različite skupove brojeva, dolazimo do skupa racionalnih brojeva kojeg označavamo slovom Q. Prirodni, cijeli brojevi, pozitivni i negativni razlomci te decimalni brojevi pripadaju skupu racionalnih brojeva Q.

Razlomci su prvi učenikov uvod u apstrakciju u matematici i kao takvi pružaju najbolji uvod u algebru u osnovnoj i srednjoj školi.Razlomcima izražavamo dio neke cjeline.
Odnosno, u matematici, razlomak je broj koji opisuje jedan ili više jednakih dijelova cjeline.

Ovdje možeš pronaći kompletnu ponudu matematičkih igračaka.

Algebarski razlomci

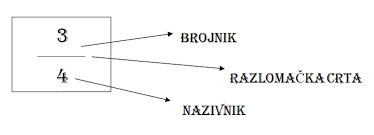
Algebarski razlomci sastoje se od brojnika, nazivnika i razlomačke crte

Rezultat dijeljenja dva prirodna broja je razlomak. Što bi značilo da gornji razlomak možemo prikazati i kao dijeljenje 3:4 odnosno ¾ .
BROJNIK – broj IZNAD razlomačke crte, u našem primjeru to je broj 3, govori nam koliko smo dijelova neke cjeline uzeli.
NAZIVNIK – broj ISPOD razlomačke crte, u našem primjeru to je broj 4, govori nam od koliko se dijelova neka cjelina sastoji.
Napisani razlomak čitamo kao TRI ČETVRTINE, a doslovno znači: tri dijela cjeline od ukupno četiri dijela.

Vrste razlomaka

Pravi - su oni razlomci kojima je brojnik manji od nazivnika ( npr. 1/4 , 2/5 ) odnosno, to je razlomak koji je manji od 1.

Nepravi - su oni razlomci kojima je brojnik veći od nazivnika (npr. 3/5 je pravi, 5/3 je nepravi razlomak) odnosno, to je razlomak koji je veći od 1.

Neprave razlomke možemo zapisati i kao MJEŠOVITE , npr. umjesto 5/3 može se pisati 1 (čita se jedno cijelo i dvije trećine, a dobije tako da izračunamo 1*3 + 2 kroz 3 ).

Recipročni - su razlomci koji se dobiju kada zamijenimo mjesta brojniku i nazivniku, npr. razlomak 3/5 recipročan je razlomku 5/3.

Dvojni - su razlomci u kojima su brojnik i nazivnik razlomci. Pojednostavljuju se u jednostavan razlomak tako da je novomu razlomku brojnik umnožak vanjskih brojeva, a nazivnik umnožak unutarnjih brojeva.

Pravila za računanje

Pri računanju s razlomcima postoji nekoliko "trikova" koji nam služe kako bi ubrzali samo rješavanje i preskočili neke korake. 

Bilo bi dobro kad bi dijete usvojilo i memoriralo ova pravila. 

Aritmetičke operacije s razlomcima

Proširivanje

Razlomak proširujemo tako da njegov brojnik i nazivnik pomnožimo nekim cijelim brojem. Prošireni razlomak je jednak početnom razlomku.

Pročitaj i naš tekst o lakšem učenju tablice množenja. 

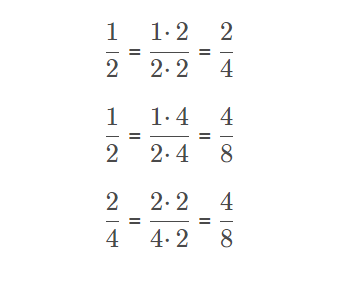
Skraćivanje

Razlomak skraćujemo tako da njegov brojnik i nazivnik podijelimo nekim cijelim brojem. U pravilu su brojnik i nazivnik djeljivi tim brojem. Skraćeni razlomak jednak je početnom razlomku.

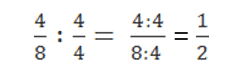
Recipročna vrijednost

Ako imamo jednostavni razlomak s brojnikom a i nazivnikom b, recipročna vrijednost iznosi mu obrnuti prikaz brojnika i nazivnika ( brojnik postaje nazivnik, a nazivnik brojnik ).

Recipročna vrijednost cijelog broja a iznosi 1/a .

Recipročna vrijednost broja oblika jednostavnog razlomka 1/a iznosi a.

Zbrajanje i oduzimanje

Prilikom zbrajanja i oduzimanja, razlomci se svode na najmanji zajednički nazivnik. On je najmanji zajednički višekratnik nazivnika tih razlomaka. Nakon svođenja na zajednički nazivnik, brojnici se zbroje ili oduzmu ovisno o operaciji.

Množenje i dijeljenje razlomaka

Razlomci se množe tako da im se pomnože brojnici te nazivnici. Umnožak brojnika postaje brojnik rezultata, a umnožak nazivnika postaje nazivnik rezultata.

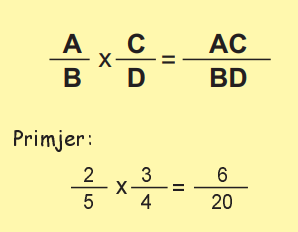
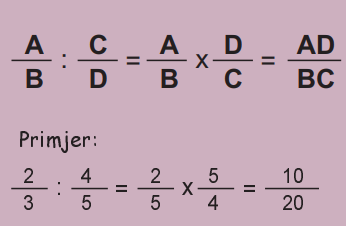
Zašto razlomci predstavljaju problem?

Mnogi će se učitelji složiti da poučavanje razlomaka može biti složeno i zbunjujuće, ali i da je razumijevanje razlomaka neophodna vještina koju učenici moraju posjedovati kako postaju stariji. Pročitala sam podatak da nakon provedenog istraživanja jedan od tri učenika ne zna poredati razlomke po veličini. To me zaista nije iznenadilo. Lako je poredati razlomke čiji su nazivnici jednaki, no problem nastaje kad treba poredati razlomke potpuno različitih brojnika i nazivnika.

Vlastito iskustvo

Što je to što razlomke čini teškim gradivom? Možda sam vizualan dojam razlomka? Broj ispod broja? Razlomačka crta? Ono što ja mogu reći iz vlastitog iskustva ( iako nisam imala poteškoća s razlomcima ) je to da mi nitko nikad nije objasnio razlomke kako treba.

Tada to nisam znala, no sada iz perspektive učitelja mislim da je vrlo važan način na koji se pojedino gradivo prezentira. Matematičari često zaboravljaju da nemaju svi isti logički „sklop“ u glavi i da nisu svima sve stvari jednako jasne. Uvjerena sam da mnogo djece ne razumije razlomke upravo iz tog razloga: LOŠE OBJAŠNJENJE.
 

Bit ću vrlo iskrena i priznati da sam nedavno doživjela „veliko prosvjetljenje“  - i kao učitelj i osobno. Među matematičkim igrama i pomagalima iz naše ponude pronašla sam jedan, naizgled jednostavan, predmet koji je zapravo vrlo, vrlo koristan -  DRVENU PLOČU S RAZLOMCIMA. Već na prvi pogled doživjela sam to svoje veliko prosvjetljenje. Pogledaj sam pa procijeni jesi li ikad razmišljao o razlomcima na ovaj način?

Zašto sam doživjela prosvjetljenje ( i ti, nadam se )? Zbog same jednostavnosti prikaza što su zapravo razlomci. To je drvena ploča s prikazanim OMJEROM razlomaka, odnosnom prikazuje nam upravo ono što razlomci i jesu – DIO NEKE CJELINE.

Preporuka matematičkih igara za učenje razlomaka

Uz pomoć ove zanimljive matematičke igre djeca će vrlo lako steći dojam u kakvom su odnosu razlomci. Zamka na koju će svako dijete pasti ( isprobaj pa ćeš vidjeti ) je kad ga pitaš : „ Hej, jel' veća jedna osmina ili jedna trećina?“. Što misliš što će odgovoriti? Gotovo svi će reći jedna osmina jer je osam veće od tri. I, pogriješiti. Djeca ne razmišljaju o tome da mi ne govorimo o prirodnim brojevima već o razlomcima te da ne vrijede ista pravila. Baš zato je važno djeci vizualno prikazati razlomke. Uz ove male kockice djeca će lako uočiti da je osmina puno manja od trećine - što je zapravo i logično, podijeli jednu cjelinu ( npr. rođendansku tortu ) na tri dijela, a drugu na osam. Koji su dijelovi veći?

Zar nije jednostavnije nego samo apstraktno zamišljati u svojim glavicama?

U našoj ponudi , osim ove genijalne igre, možeš još pronaći i igru s dijelovima kruga koji prikazuju upravo ono što djeca moraju vizualno shvatiti: da su razlomci dijelovi cjeline. 

Dijelovi kruga - učenje razlomaka

Drvena ploča s razlomcima

Tekstovi koji bi te mogli zanimati:

- 5 trikova za učenje tablice množenja

- 10 trikova za crtanje životinja

- Piramida zdrave hrane

Zaključak

Apstraktni pojmovi kao što su razlomci koje učenici ne svladaju u ranim razredima mogu ih kasnije zbuniti i izazvati velike probleme. Neki stručnjaci smatraju razumijevanje razlomaka kao vrata za kasnije učenje matematike i kao temelj naprednijih matematičkih i prirodnih znanosti kao što su algebra, geometrija, statistika, kemija i fizika.

Ono što bi uvelike olakšalo samo razumijevanje razlomaka je upravo vizualizacija istih. Važno je djeci predočiti razlomke kao dijelove cjeline, prikazati im na primjeru što znači brojnik, a što nazivnik. Na taj način bit će im jasniji zadaci koji se od njih traže, znat će usporediti razlomke kao i izračunati matematičke operacije. To i je smisao razumijevanja razlomaka;  dobar temelj za nadogradnju matematičkih znanja.